Proof and Learning
Table of Contents
Meditations from my transition from math academia to industry. Mentions my current labor-of-love, an experimental optimization crate.
Proof, a social game
In academia
It's 2023 and Terence Tao is formalizing theorems with software. Mathematics will probably change when simulation becomes a viable medium to faciliate rigorous, open-ended problem-solving.
Even mathematical proof, with formally stated theorems, is a social game. For minor results, convince your team, yourself, and the reviewers of a few claims. Do this by sandwiching formal arguments in a document prepared by code in an archaic scripting language. For major results, convince the community, too.
Mathematical papers go like this. Expose key ideas. Factor prose from proof. Invert the creative meander into an enumerated syllogism. Encapsulate grimy lemmas so the poor reader can take a break.
It's a synthesis of communication and formalism. A necessary, but exhausting labor for the academic who is always expected to produce output. But sometimes communication fails. And sometimes the formalism falls apart.
Computers have been helping us since the Appel-Haken proof of the $4$-Color Theorem. It took a decade to retract the flawed, computer-less proofs.
What role will computers play in math in the coming years?
In industry
I have a practical question:
How does a researcher with a decade of experience developing ad hoc solutions with whatever-tool-it-takes find a team that values her creativity, growth, and passion for collaborate problem-solving?
In industry, the burden of proof is different. Like math, it's not all about formalism. My first "resume" was a stack of 200 pages of published research and a 7-page CV. Ha!
To communicate, build projects, push commits, and make some pretty graphics. Find community, collaborate, and get lucky. At least, that's what I'm trying. Like math, it's not always going to work. Like math, it mostly doesn't. So try new things, but take care of yourself too.
Learning from states and actions
As an academic
My best ideas come from data.
I used to write so much SageMath. So many Jupyter notebooks full of dynamic programs, print statements, plots. All for my mathematical experiments. Lost to the time before I understood version control.
My learning loop consisted (partly) of:
- (perform a search) trying to prove from first principles
- (visualize data) plotting computational evidence
- (make predictions) extrapolating from datasets and plots
- (calculate loss) making enthusiastic claims
- (backprop gradients) sheepishly email teammates about my miscalcuations
This worked surprisingly well, and made collaborators and mentors chuckle. After all, there is no closed-form solution to explore-exploit dilemma. Everyone has their own approach. Try everything. Measure what you can.
In deep reinforcement learning
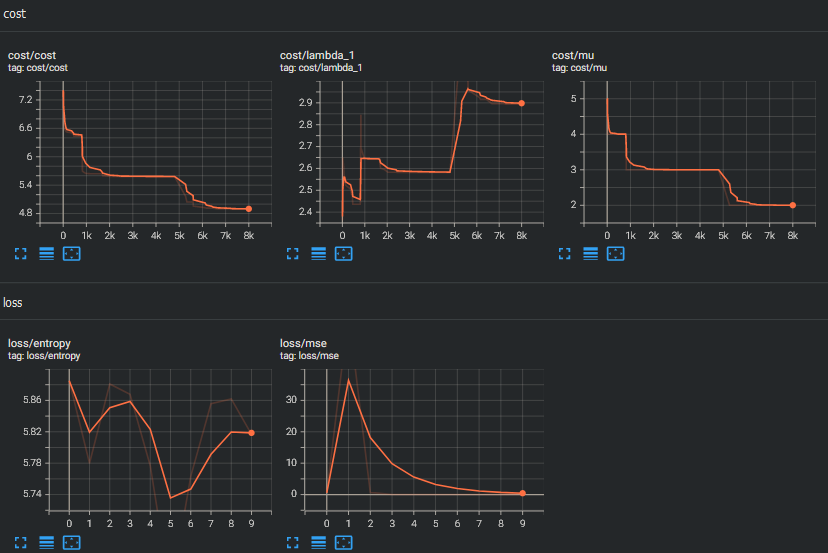
I like reinforcement learning, but I know I'm only scratching the surface. My data-parallel optimization crate has an MVP and probably needs a new name. Maybe azdo.
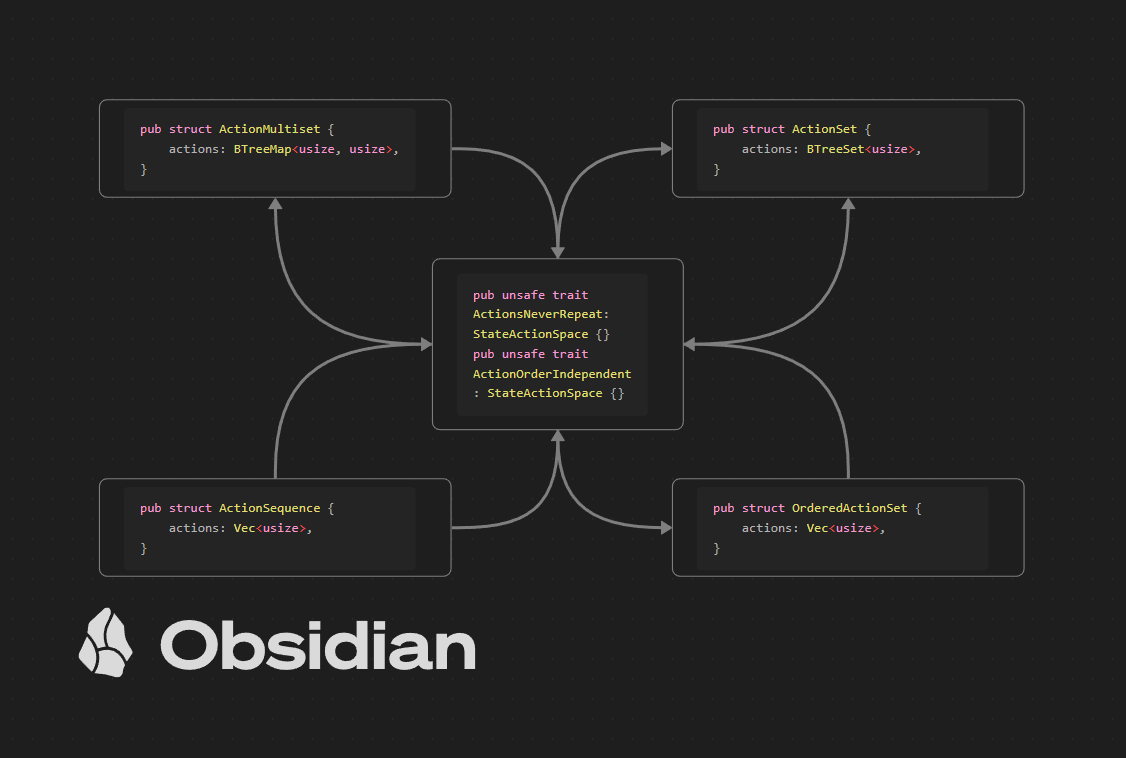
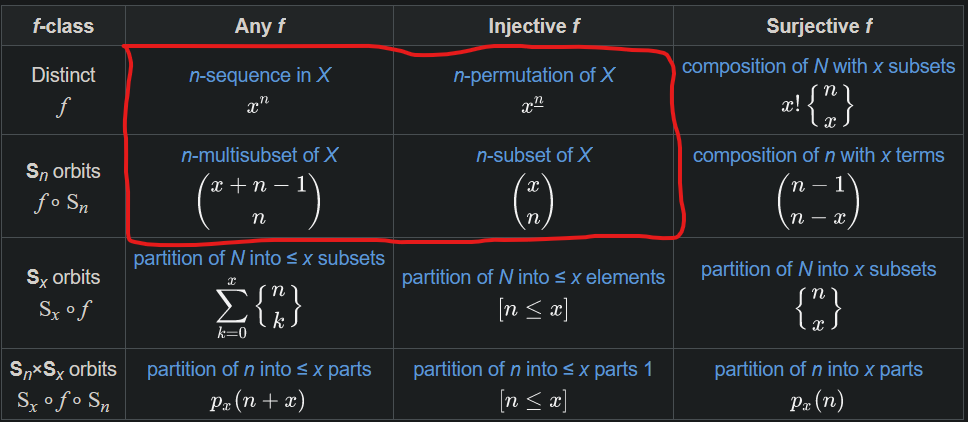
It has some helper traits which form a $2\times 2$ grid of derived impls. If you squint, you'll find this block in the top-left corner of the $12$-fold way table. An ergonomic way to reduce combinatorial explosion in the size of Monte Carlo search trees.
What I love about implementing these algorithms is simple:
unlike pure math, progress can be clearly measured
Searches produce concrete structures, plottable data, prediction functions, and numerical loss. You can even adjust behavior in real-time.
So far:
- It refutes Conjecture 2.1 (previously refuted by Wagner with the cross entropy method) in only one minute.
- It's riddled with a list of desired features I have publicly externalized.
Offline progress continues in the privately externalized backburner (read: Obsidian canvases).
For now
I have been:
- chewing on a novel problem space
- taking a healthy break
- visiting loved ones
- skimming papers and blogs
- making new connections.
I'm optimistic. If that changes, I have a practical job search optimization algorithm I can refactor.